This work is aimed at helping to understand the representations that facilitate visual object recognition in the ventral stream of the primate visual system. The task of this stream can be expressed as retrieving from memory a semantic meaning or label that can be attached to a particular object in a visual scene. This task describes both recognition and categorization. The types of labels used depend on what level of detail is desired, and here we have chosen to focus on subordinate-level categorization, and individual exemplar recognition. Our approach can be described in terms of three questions that we want to address: first what is the representation, secondly how is the representation used, or what are the computations that the brain performs on the representation, and thirdly where is the representation located in the brain. We hope to combine the different strengths of psychophysics, computational modeling, and function brain imaging to address these questions.

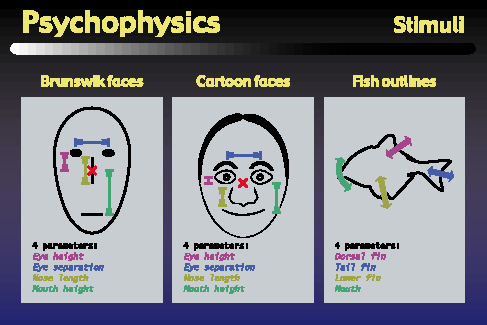
Our psychophysics approach used these three sets of visual stimuli in our psychophysics and functional brain imaging experiments. Each set consisted of twenty objects, parameterized along four dimensions, although it should be noted that our subjects were never told about these dimensions. We began by using the well-known Brunswik faces which are parameterized by eye height, eye separation, nose length, and mouth height. We have also used a set of more realistic looking faces that were developed in our lab, which are actually defined by 28 parameters, although for these experiments, we varied only the four parameters that correspond to the Brunswik face parameters. Finally, we have also developed a set of novel stimuli based on the silhouettes of tropical fish. These objects also have four parameters which control the Bezier curves that define the fishes' dorsal fin, tail fin, lower fin, and mouth or snout area.

The first type of psychophysics task that we performed was a similiarity task that was designed to generate data that could be used to fit multidimensional scaling models. We used two versions of this task: one was a pairs task, in which subjects viewed pairs of objects, and assigned ratings between 1 and 9 indicating how similar the objects appeared. The second task was a triads task, in which subjects viewed triplets of objects, and answered whether the left or right pair of objects appeared more similar. Although either task might be sufficient on its own, we chose to directly compare both, since each task has different advantages for us. The advantage of the triads task is that it can be learned by monkeys, and similar experiments to those shown here are being carried out in the laboratory of Dr. Nikos Logothetis at the Max Planck Institute in Tuebingen, Germany. However, human subjects prefer the pairs task because it is more natural and requires many fewer trials than the triads task. So, in order to facilitate future comparisons between monkey and human data, we wanted to begin with a direct comparison in human subjects between the pairs and triads tasks.

The second type of psychophysics task that we performed was a classification task. For this task, the 20 objects of each object set were split into ten training exemplars and ten testing exemplars. The ten training exemplars were assigned to two linearly separable categories. The right side of the figure above shows the arrangement of training exemplars that we used for all three object sets. The top graph shows the locations of the training exemplars along dimensions one and two, while the lower graph shows their locations along dimensions three and four. The classification task itself consisted of a training phase, in which subjects learned to categorize the training exemplars at 85% accuracy, and a testing phase, in which subjects categorized both the training and the testing exemplars. The frequencies with which subjects assigned the objects to category one or category two were used to fit the classification models which are described later.

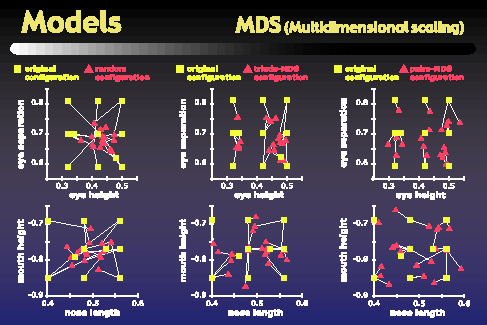
Our modeling work began with a multidimensional scaling analysis that we applied to the data from the psychophysics similarity tasks. These MDS analyses attempted to assign each object to a location in a four-dimensional space such that the distances between objects in this space correlate well with the similarities obtained in the psychophysics similarity tasks. One of the questions we wanted to address was how similar the MDS spaces are to the original parameter space in which the objects were defined. To get at this, we used the Procrustes transform to put our MDS spaces into best alignment with the original parameter space. The plots on the figure above show the locations of objects both in the original parameter space, in green, as well as in the Procrustes-transformed MDS spaces, in red. The top plots show dimensions one and two, and the bottom plots show dimensions three and four. The left column actually shows a random configuration that has been Procrustes-transformed into best alignment with the original parameter space, while the center column shows an MDS space based on a single subject's triads task, and the right column shows the MDS space based on that subject's pairs task. As the figure shows, the alignment between green and red dots is better for the MDS configurations than it is for the random configuration.

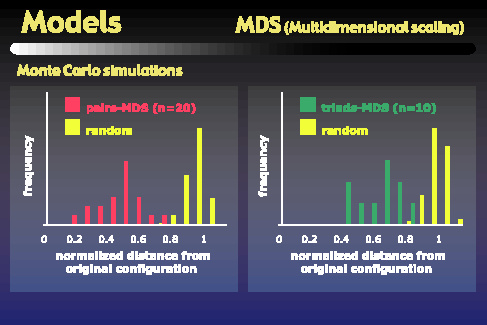
In order to quantify this effect, we ran Monte Carlo simulations comparing the distances of random configurations from the original space to the distances of our subjects' MDS configurations from the original space. These graphs show the distributions of those distances. The left graph shows the peak of the pairs-based MDS distribution is roughly twice as close to the original configuration as would be expected by chance. The right plot shows that the triads-based MDS configurations are also significantly closer to the original space than would be expected by chance, but not as close as are the pairs-based MDS configurations.

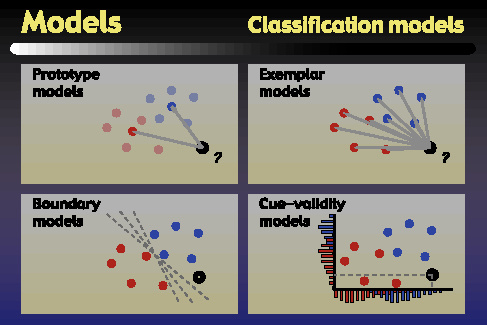
The second part of our modeling studies attempted to explain subjects' performance in the classification task. The four classes of models that we examined are depicted in schematic form in the above figure. The first class was prototype models, which remember a prototype as the average of all training exemplars for a category. A test object is classified into the category whose prototype is nearer to that object. The second model type was exemplar models, which compute the average distance of a test object to each of the exemplars in a category, and classify the test object into the category for which this average distance is smallest. The third model type was the boundary or linear classifier model, in which the model learns a boundary that separates the categories, and classifies test objects according to which side of the boundary they fall on. Finally, we considered cue-validity models. In these models, the validity of a parameter value for a particular category is just the conditional probability of that parameter value coming from an object in the given category. Test objects are classified into the category with the higher average validity across the four parameters.

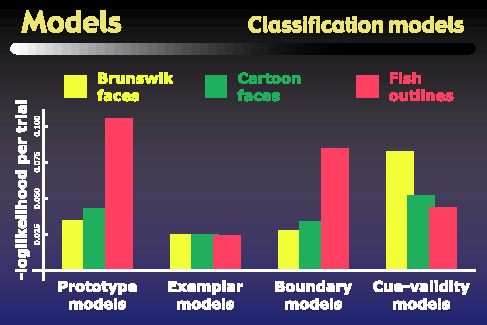
We tested the models using both the original parameter space as well as MDS spaces for the representation of the objects, but we found that both the triads- and pairs-based MDS spaces gave the same pattern of model performances as did the original parameter space. This figure summarizes the performance of the four model types based in the original parameter space, for each of the three object types. The y-axis gives the measure that was minimized to fit the models, such that a smaller value means that the model achieved a better fit to subjects' psychophysical data. The main result we observed is that the exemplar models give the best fit for all three object classes. For the face objects, the boundary models also perform quite well, and in fact are statistically indistinguishable from the exemplar models. However the prototype models perform statistically significantly worse than exemplar models for all object classes. The other interesting result is the striking difference between the pattern of performances on the fish outlines versus either set of faces. For example, while the cue validity models gave the worst performance for the faces, they give the second best performance on the fish outlines, and are in fact statistically indistinguishable from the exemplar models for these stimuli. On the other hand, the performance of the prototype model is even worse for the fish outlines than it is for the face objects.

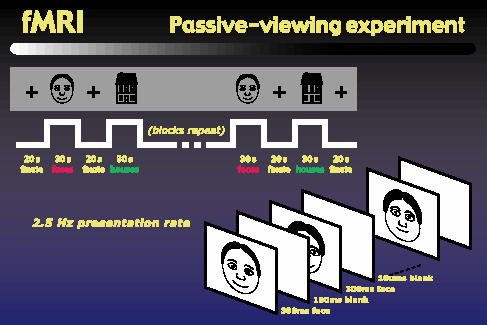
Finally, we started a series of fMRI experiments to help address the question of where the object representations occur in the brain. We began with a block-design passive-viewing experiment similar to those used by Kanwisher and others. Subjects view blocks of rapidly presented objects, alternating with fixation intervals. The objects blocks alternate between faces and houses. We performed this experiment using photographs of real faces, Brunswik faces, and our cartoon faces, each matched with a corresponding set of house images.

As others have reported, when we look for regions that are more active during face viewing than during house viewing, we find centers of activity in the middle fusiform gyrus, or fusiform face area, as well as in the lateral occipital gyrus. These activity centers, shown here for a single subject, are found bilaterally, giving us four potential regions of interest: left and right FFA, and left and right LO.

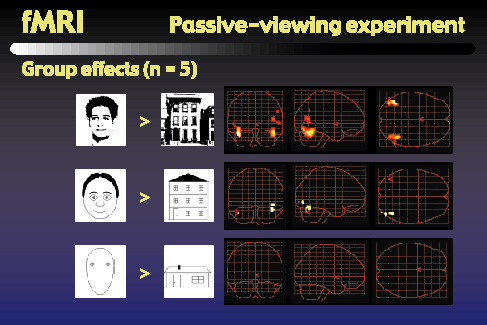
This figure shows the results of a group analysis for the different types of faces and houses that we used. These glass brain views show the regions that were more active when subjects viewed the faces than when they viewed the houses. The top row shows bilateral activation in both FFA and LO when we use photos of real faces and real houses. As the middle row shows, when we use the cartoon faces along with line-drawn houses, we find reduced but still significant contrast in the right FFA and right LO, but the contrast in left LO is only marginally significant, and the contrast in left FFA has vanished. Going to the bottom row, we can see that when we use the Brunswik faces along with very simple line-drawn houses, we found no significant contrast between the face and house activity in any of the four regions of interest.

Let's go back to the three questions posed at the beginning. What is the representation? Our similarity task and MDS models suggest that subjects' internal representations are flexible, as they adapt to previously unseen classes of objects. In addition, we found that subjects' internal representations spaces faithfully reflect the external parameters of variability that were present in the objects. Future human fMRI and monkey electrophysiology studies will attempt to provide direct evidence to support these claims about internal representations. How is the representation used? We found clear evidence that for all object classes, subjects' performance is better described by exemplar models than by prototype models. It is somewhat surprising that exemplar models fit well with human behavior, since this implies unbounded memory demands as category size increases. Others have shown category prototypes to be better recognized with larger categories, so in the future, we will consider models that can accommodate those results as well as our own by interpolating between exemplar-based and prototype-based categorization. The differences between the model-fits for face and fish objects may reflect the difference in subjects' expertise with these different types of objects: while subjects have had lifelong experience viewing and categorizing faces, they had never before seen these fish stimuli. Where is the representation located? Our initial fMRI work has shown that cartoon faces give rise to activity in the same areas as do real faces, but that the level of activity is dependent on the level of detail in the cartoon faces. This provides a basis for future work to investigate more closely the representations and computations that may be carried out in the regions of interest that we have identified.