

For a good summary of the story which does not require any maths background, have a look at two press releases by Eric Mankin here and here.
| The concept of surprise is central to sensory processing, adaptation and learning, attention, and decision making. Yet, until now, no widely-accepted mathematical theory existed to quantify surprise elicited by stimuli or events, for observers ranging from single neurons to complex natural or engineered systems. In work in collaboration with Prof. Pierre Baldi at the University of California at Irvine, we have developed a formal Bayesian definition of surprise that is the only consistent formulation under minimal axiomatic assumptions. Bayesian surprise quantifies how data affects natural or artificial observers, by measuring differences between posterior and prior beliefs of the observers. Using this framework we tested whether humans orient their gaze towards surprising events or items while watching television. Bayesian surprise strongly attracts human observers, with 72% of all gaze shifts directed towards locations more surprising than the average, a figure rising to 84% when considering only gaze targets simultaneously selected by all subjects. The resulting theory of surprise is applicable across different spatio-temporal scales, modalities, and levels of abstraction. |  |
We propose that surprise is a general, information-theoretic concept, which can be derived from first principles and formalized analytically across spatio-temporal scales, sensory modalities, and, more generally, data types and data sources. Two elements are essential for a principled definition of surprise. First, surprise can exist only in the presence of uncertainty, which can arise from intrinsic stochasticity, missing information, or limited computing resources. A world that is purely deterministic and predictable in real-time for a given observer contains no surprises. Second, surprise can only be defined in a relative, subjective, manner and is related to the expectations of the observer, be it a single synapse, neuronal circuit, organism, or computer device. The same data may carry different amounts of surprise for different observers, or even for the same observer taken at different times.
In probability and decision theory it can be shown that, under a small set of axioms, the only consistent way for modeling and reasoning about uncertainty is provided by the Bayesian theory of probability. Furthermore, in the Bayesian framework, probabilities correspond to subjective degrees of beliefs in hypotheses or models which are updated, as data is acquired, using Bayes' theorem as the fundamental tool for transforming prior belief distributions into posterior belief distributions. Therefore, within the same optimal framework, the only consistent definition of surprise must involve: (1) probabilistic concepts to cope with uncertainty; and (2) prior and posterior distributions to capture subjective expectations.
Specifically, the background information of an observer is captured by his/her/its prior probability distribution:
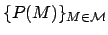
over the hypotheses or models M in a model space. Given such a prior distribution of beliefs, the fundamental effect of a new data observation D on the observer is to change the prior distribution {P(M)} (for all models M in the model space) into the posterior distribution {P(M|D)} via Bayes' theorem, whereby:
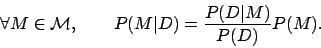
In this framework, the new data observation D carries no surprise if it leaves the observer's beliefs unaffected, that is, if the posterior is identical to the prior; conversely, D is surprising if the posterior distribution resulting from observing D significantly differs from the prior distribution. Therefore we formally measure surprise elicited by quantifying the distance (or dissimilarity) between the posterior and prior distributions. This is best done using the relative entropy or Kullback-Leibler (KL) divergence. Thus, surprise is defined by the average of the log-odd ratio:
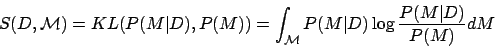
taken with respect to the posterior distribution over the model space. Note that KL is not symmetric but has well-known theoretical advantages, including invariance with respect to reparameterizations. A unit of surprise --- a wow --- may then be defined for a single model M as the amount of surprise corresponding to a two-fold variation between P(M|D) and P(M), i.e., as log P(M|D)/P(M) (with log taken in base 2). The total number of wows experienced when simultaneously considering all models is obtained through the integration over the model class.
|
To illustrate how surprise arises when data is observed, consider a human observer who just turned a television set on, not knowing which channel it is tuned to. The observer has a number of co-existing hypotheses or models about which channel may be on, for example, MTV, CNN, FOX, BBC, etc. (figure). Over the course of viewing the first few video frames of the unknown channel (here, CNN), the observer's beliefs in each hypothesis adjust, progressively favoring one channel over the others (leading to a higher prior probability for CNN in left panel). Consider next what happens if yet another video frame of the same program is observed (top right), intuitively an unsurprising event. Through Bayesian update, the new frame only minimally alters the observer's beliefs, with the posterior distribution of beliefs over models showing a slightly reinforced belief into the correct channel at the expense of the others. In contrast, if a frame of snow was suddenly observed (middle right), intuitively this should be a very surprising event, as it may signal storm, earthquake, toddler's curiosity, electronic malfunction, or a military putsch. Through Bayesian update, this observation would yield a large shift between the prior and posterior distributions of beliefs, with the posterior now strongly favoring a snow model (and possible associated earthquake, malfunction, etc. hypotheses), correspondingly reducing belief in all other television channels. In sum, unsurprising data yields little difference between posterior and prior distributions of beliefs over models, while surprising data yields a large shift: in mathematical terms, an event is surprising when the distance between posterior and prior distributions of beliefs over all models is large. |
|
While at onset snow is surprising (above figure, middle right), after sustained viewing it quickly becomes boring to most humans. Indeed, no more surprise arises after the observer's beliefs have stabilized towards strongly favoring the snow model over all others (above figure, bottom right). Thus surprise resolves the classical paradox that random snow, although in the long term the most boring of all television programs, carries the largest amount of Shannon information. This paradox arises from the fact that there are many more possible random images than there exists natural images. Thus, the entropy of snow is higher than that of natural scenes. Even when the observer knows to expect snow, every individual frame of snow carries a large amount of Shannon information.
Indeed, in a sample recording of 20,000 video frames from typical television programs, presumably of interest to millions of watchers, we measured approximately 20 times less Shannon information per second than in matched random snow clips, after compression to constant-quality MPEG4 to adaptively eliminate redundancy in both cases (table below). The situation was reversed when we measured that snow clips carried about 17 times less surprise per second than the television clips, evaluated using the average, over space and time, of the output of the surprise metric presented with our human experiments. Thus, more informative data may not always be more important, interesting, worthy of attention, or surprising.
| TV | Snow | TV:Snow Ratio | |
| Shannon Information (Mbytes/s) | 0.25 +/- 0.16 | 4.90 +/- 0.01 | 1:20 |
| Surprise (wows/s) | 50.83 +/- 0.43 | 2.99 +/- 0.02 | 17:1 |
To test the surprise hypothesis --- that Bayesian surprise attracts human attention in dynamic natural scenes --- we recorded eye movements from eight naive observers. Each watched a subset (about half) from 50 videoclips totaling over 25 minutes of playtime. Clips comprised outdoors daytime and nighttime scenes of crowded environments, video games, and television broadcast including news, sports, and commercials. Right-eye position was tracked with a 240Hz video-based device. Observers were instructed to follow the stimuli's main actors and actions, so that their gaze shifts reflected an active search for nonspecific information of subjective interest. Two hundred calibrated eye movement traces (10,192 saccades) were analyzed, corresponding to four distinct observers for each of the 50 clips.
To characterize image regions selected by participants, we process videoclips through computational metrics that output a topographic dynamic master response map, assigning in real-time a response value to every input location. A good master map would highlight, more than expected by chance, locations gazed to by observers. To score each metric we hence sample, at onset of every human saccade, master map activity around the saccade's future endpoint, and around a uniformly random endpoint (random sampling was repeated 100 times to evaluate variability). We quantify differences between histograms of master map samples collected from human and random saccades using again the Kullback-Leibler (KL) distance: metrics which better predict human scanpaths exhibit higher distances from random. This scoring presents several advantages over simpler scoring schemes, including agnosticity to putative mechanisms for generating saccades and the fact that applying any continuous nonlinearity to master map values would not affect scoring.
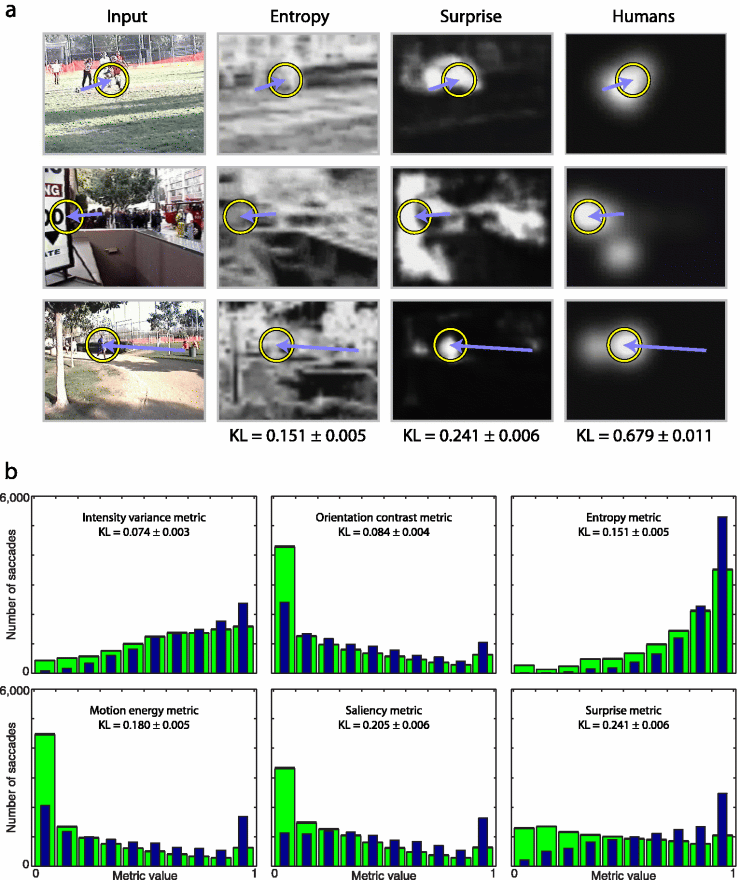 |
The surprise metric used here quantifies low-level surprise in image patches over space and time, and at this point does not account for cognitive beliefs of our human observers, nor does it attempt to consider high-level, possibly semantically-rich, models for the video frames (such as the models of television channels discussed above). Yet, We find that the surprise metric significantly outperforms all other computational metrics tested, scoring nearly 20% better than the second-best metric (saliency) and 60% better than the best static metric (Shannon entropy).
The definition of surprise --- as the distance between the posterior and prior distributions of beliefs over models --- is entirely general and readily applicable to the analysis of auditory, olfactory, gustatory, or somatosensory data. While here we have focused on behavior rather than detailed biophysical implementation, it is worth noting that detecting surprise in neural spike trains does not require semantic understanding of the data carried by the spike trains, and thus could provide guiding signals during self-organization and development of sensory areas.
At higher processing levels, top-down cues and task demands are known to combine with stimulus novelty in capturing attention and triggering learning, ideas which may now be formalized and quantified in terms of priors, posteriors, and surprise. For instance, surprise theory can further be tested and utilized in experiments where the prior is biased by top-down instructions or prior exposures to stimuli. In addition, surprise-based behavioral measures, such as the eye-tracking one used here, may prove useful for early diagnostic of human conditions including autism and attention-deficit hyperactive disorder (ADHD), as well as for quantitative comparison between humans and animals which may have lower or different priors, including monkeys, frogs, and flies. Beyond sensory neurobiology and human psychology, computable surprise could guide the development of data mining and compression systems (allocating more resources to surprising regions of interest, see here), to find surprising agents in crowds, surprising sentences in books or speeches, surprising medical symptoms, surprising odors in airport luggage racks, surprising documents on the world-wide-web, or to design surprising advertisements.
Copyright © 2006 by the University of Southern California, iLab and Prof. Laurent Itti