MathFunctions.H File Reference

#include "Util/Assert.H"
#include "Image/Image.H"
#include "Image/Point2D.H"
#include "Util/FastMathFunctions.H"
#include "Util/Promotions.H"
#include "rutz/compat_cmath.h"
#include <algorithm>
#include <cmath>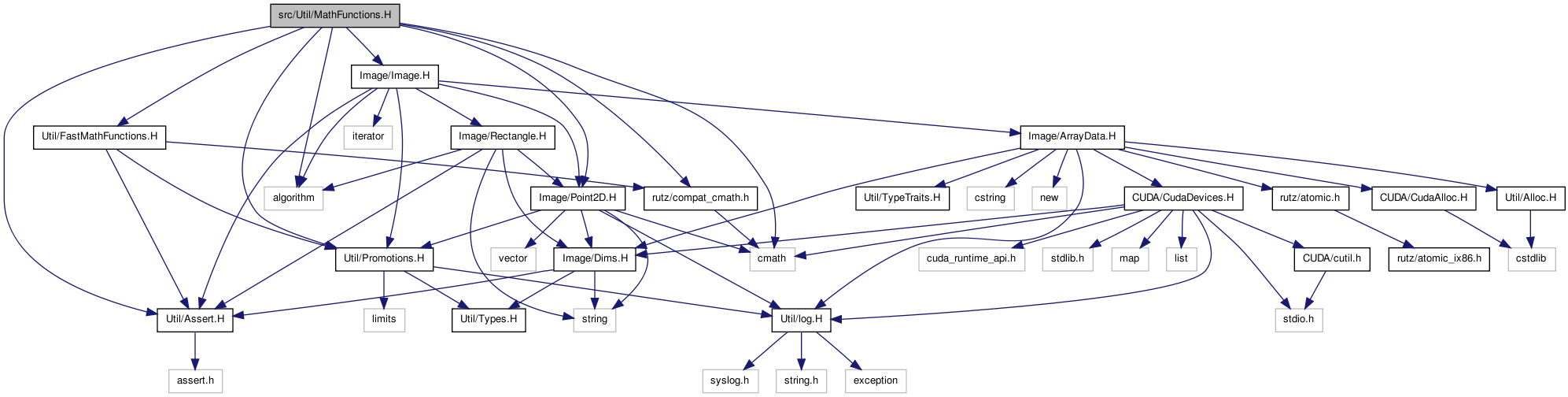
Include dependency graph for MathFunctions.H:

Go to the source code of this file.

Classes

struct  cheb_series_struct
struct  GaussianDef
 Definition for a gaussian used for GMM. More...

Defines

#define D_PI   3.1415926535897932384626433832795029
 Miscellaneous math functions.
#define D_E   2.7182818284590452353602874713526625
 e
#define D_LOG_SQRT_2_PI   0.9189385332046727417803297364056176
 Log Root of 2 Pi.
#define D_SQRT_2_PI   2.5066282746310002416123552393401041
 Root of 2*Pi.
#define D_SQRT_PI   1.7724538509055160272981674833411451
 Root of Pi.
#define D_SQRT_2   1.4142135623730950488016887242096981
 Root of 2 DEFINED in cmath as M_SQRT2, but is not 128 bit.
#define D_LOG_2_PI   1.8378770664093454835606594728112353
 Natural Log of 2*Pi.
#define D_LOG_PI   1.1447298858494001741434273513530587
 Natural Log of Pi.
#define D_LOG_2   0.6931471805599453094172321214581766
 Natural Log of 2 DEFINED in cmath as M_LN2, but is not 128 bit.
#define D_LOG_SQRT_2   0.3465735902799726547086160607290883
 Natural Log of sqrt of 2.
#define D_2_PI   6.2831853071795862319959269370883703
 2*Pi
#define D_EULER_GAMMA   0.5772156649015328606065120900824024
 The Euler-Mascheroni Constant (Not the same as e).
#define D_DEGREE   0.0174532925199432957692369076848861
 Number of radians in one degree.
#define D_GOLDEN_RATIO   1.6180339887498948482045868343656381
 The golden ratio.
#define D_CATALAN   0.9159655941772190150546035149323841
 Catalan's Constant.
#define D_GLAISHER   1.2824271291006226368753425688697917
 Glaisher-Kinkelin Constant.
#define D_KHINCHIN   2.6854520010653064453097148354817956
 Khinchin's Constant.
#define D_SOLDNER   1.4513692348833810502839684858920274
 Ramanujan-Soldner's Constant.
#define D_APERY   1.2020569031595942853997381615114499
 Apery's Constant.
#define D_GAUSS_KUZMAN   0.3036630028987326585974481219015562
 Gauss-Kuzmin-Wirsing constant.
#define D_FRANSEN   2.8077702420285193652215011865577729
 Fransén-Robinson constant.
#define D_SERPINSKY   2.5849817595792532170658935873831711
 Sierpin'ski's constant.
#define D_MILL   1.3063778838630806904686144926026057
 Mills' constant.
#define D_OMEGA   0.5671432904097838729999686622103555
 Omega constant.
#define D_GOLOMB_DICKMAN   0.6243299885435508709929363831008372
 Golomb-Dickman constant.
#define L_PI   3.14159265358979323846264338327950288419716939937510582097494459230781L
 Pi.
#define L_E   2.71828182845904523536028747135266249775724709369995957496696762772407L
 e
#define L_LOG_SQRT_2_PI   0.91893853320467274178032973640561763986139747363778341281715154048276L
 Log Root of 2 Pi.
#define L_SQRT_2_PI   2.50662827463100050241576528481104525300698674060993831662992357634229L
 Root of 2*Pi.
#define L_SQRT_PI   1.77245385090551602729816748334114518279754945612238712821380778985291L
 Root of Pi.
#define L_SQRT_2   1.41421356237309514547462185873882845044136047363281250000000000000000L
 Root of 2 DEFINED in cmath as M_SQRT2, but is not > 128 bit.
#define L_LOG_2_PI   1.83787706640934548356065947281123527972279494727556682563430308096553L
 Natural Log of 2*Pi.
#define L_LOG_PI   1.14472988584940017414342735135305871164729481291531157151362307147214L
 Natural Log of Pi.
#define L_LOG_2   0.69314718055994528622676398299518041312694549560546875000000000000000L
 Natural Log of 2 DEFINED in cmath as M_LN2, but is not > 128 bit.
#define L_2_PI   6.28318530717958647692528676655900576839433879875021164194988918461560L
 2*Pi
#define L_DEGREE   0.01745329251994329576923690768488612713442871888541725456097191440171L
 Number of radians in one degree.
#define L_EULER_GAMMA   0.57721566490153286060651209008240243104215933593992359880576723488486L
 The Euler-Mascheroni Constant (Not the same as e).
#define L_GOLDEN_RATIO   1.61803398874989484820458683436563811772030917980576286213544862270526L
 The golden ratio.
#define L_CATALAN   0.91596559417721901505460351493238411077414937428167213426649811962176L
 Catalan's Constant.
#define L_GLAISHER   1.28242712910062263687534256886979172776768892732500119206374002174040L
 Glaisher-Kinkelin Constant.
#define L_KHINCHIN   2.68545200106530644530971483548179569382038229399446295305115234555721L
 Khinchin's Constant.

Typedefs

typedef struct cheb_series_struct cheb_series

Functions

template<class T >
T onlineMean (T mu, T A, int n)
template<class T >
T onlineStdev (T mu, T stdev, T A, int n)
double cheb_eval (const cheb_series *cs, const double x)
double cheb_eval_psi (const double x)
double cheb_eval_apsi (const double x)
double fast_psi (const double x)
template<class T >
T wow (const T &k)
 Convert a number into Wows, for instance a KL distance.
template<class T >
T KLjointGammaGamma (const T ai, const T aj, const T bi, const T bj, const T Ai, const T Aj, const T Bi, const T Bj, const bool doWow=false, const T gammaBiasi=1.0F, const T gammaBiasj=1.0F)
 Compute the KL distance for a joint gamma PDF.
template<class T >
T KLjointGammaGauss (const T a, const T u, const T b, const T s, const T A, const T U, const T B, const T S, const bool doWow=false, const T gammaBias=1.0F, const T gaussBias=1.0F)
 Compute the KL distance for a joint gamma gauss PDF.
template<class T >
T KLgamma (const T a, const T b, const T A, const T B, const bool doWow=false)
 Compute the KL distance for a single gamma PDF.
template<class T >
T KLgammaConst (const T a, const T A, const T C1, const T C2, const bool doWow=false)
 Compute the KL distance for a single gamma PDF.
template<class T >
T KLgamma (const T a, const T A, const bool doWow=false)
 Compute the KL distance for a single gamma PDF.
template<class T >
T KLgauss (const T u, const T s, const T U, const T S, const bool doWow=false)
 Compute the KL distance for a single gauss PDF.
double L2GMM (const std::vector< GaussianDef > &f, const std::vector< GaussianDef > &g)
 Compute the L2 distance between two mixtures of Gaussians.
double AUC (const float *model, const float *rand, size_t sm, size_t sr, const double step=0.1)
template<class T >
Point2D< T > ellipsoid (const T a, const T b, const T e, const T theta)
Point2D< float > getEllipseFromCov (const Image< double > &cov)
 Convert from a covariance matrix to the major/minor axis of an ellipse.
double getChi2Inv (int k)
 A table for returning the chi2inv at 95% (should be expanded as needed).
Basic numerical operations

template<class T >
int signOf (const T &x)
 Returns -1 if x is negative, or 1 if x is positve.
template<class T >
T squareOf (const T &x)
 Returns the square of x.
template<class T , class T2 >
T clampValue (const T &val, const T2 &bound1, const T2 &bound2)
 Returns the number closest to val and between bound1 and bound2.
Numerical range and finiteness testing

bool isFinite (const byte &arg)
 Function to check for finite value.
bool isFinite (const int16 &arg)
 Function to check for finite value.
bool isFinite (const int32 &arg)
 Function to check for finite value.
bool isFinite (const float &arg)
 Function to check for finite value.
bool isFinite (const double &arg)
 Function to check for finite value.
Random number generation

void initRandomNumbers ()
 Initialize random seeds from pseudo-random sources (e.g. time(), getpid()).
void initRandomNumbersZero ()
 Initialize random seeds with zero, to produce deterministic pseudo-random sequences.
double randomDouble ()
 Generate a random double in [0.0,1.0).
double randomDoubleFromNormal (const double s)
 Generate a random double from a normal distribution with mean zero and standard deviation s.
int randomUpToIncluding (const int n)
 Generate a random integer in [0,n] (i.e., including n).
int randomUpToNotIncluding (const int n)
 Generate a random integer in [0,n) (i.e., not including n).
template<class T >
void randShuffle (T *array, const uint size)
 Randomly shuffle given array.
double ran2 (int &idum)
 Random number generator from Numerical Recipes in C book.
int getIdum (const bool useRandom=true)
 Get a random seed for ran2.
double gasdev (int &idum)
 Randomly distributed Gaussian deviate with zero mean and unit variance.
double expdev (int &idum)
 Randomly distributed Exponential deviate.
Special math functions with iterative implementations

double poisson (const unsigned int k, const double mu)
 Compute probability of drawing a value k from a Poisson of mean mu.
double lngamma (double x)
 Compute log of Gamma.
double psi (const double x)
 Compute the psi (derivarive of log of gamma) function (requires x > 0.0).
Scalar math functions corresponding with Pixel math functions in Pixels.h

template<class T >
T maxmerge (T A, const T B)
template<class T >
T minmerge (T A, const T B)
template<class T >
T sec (T A)
 Secant.
template<class T >
T cosec (T A)
 Cosecant.
template<class T >
T cotan (T A)
 Cotangent.
template<class T >
T asec (T A)
 inverse secant
template<class T >
T acosec (T A)
 inverse cosecant
template<class T >
T acotan (T A)
 inverse cotangent
template<class T >
T sech (T A)
 Hyperbolic Secant.
template<class T >
T cosech (T A)
 Hyperbolic Cosecant.
template<class T >
T cotanh (T A)
 Hyperbolic Cotangent.
template<class T >
T asech (T A)
 Inverse Hyperbolic Secant.
template<class T >
T acosech (T A)
 Inverse Hyperbolic Cosecant.
template<class T >
T acotanh (T A)
 Inverse Hyperbolic Cotangent.
template<class T >
T sign (T A)
 return the sign of this item
template<class T >
T logN (T A, const T n)
 logN for pixel
template<class T >
T logsig (T A, const T a, const T b)
 log sigmoid for pixel
template<class T >
T logsig2 (T x, const T a, const T b)
 log sigmoid for pixel with offset
template<class T >
T tansig (T A)
 tan sigmoid for pixel
template<class T >
T angDiff (const T A, const T B, const double diffWRAP=M_PI)
 Angle difference, which is the minimum circular difference between two angles. Angles are in rad. Only for angles from 0 to diffWRAP.
template<class T >
double angle (const Point2D< T > p0, const Point2D< T > p1, const Point2D< T > p2)
 Find the cosine of the angle between two vectors (p0,p1) and (p0,p2).
template<class T >
T saturate (T A, const T n)
 saturate pixel at some value
template<class T >
T gauss (T A, const T Mu, const T Std)
 find p from a Gaussian distribution
template<class T >
T gauss (T diff, const T Std)
template<class T >
T gamma (T X, const T A, const T B)
 find p from a gamma distrabution
template<class T >
T max (T A)
 this nonsense operator is for compatability
template<class T >
T min (T A)
 this nonsense operator is for compatability
template<class T >
bool isBounded (T A, const T upper, const T lower)
 find if this value or pixel is bounded by the other two
template<class T >
T sum (T A)
 this nonsense operator is for compatability
template<class T >
T mean (T A)
 this nonsense operator is for compatability

Variables

static double psics_data [23]
static const cheb_series psi_cs = { psics_data, 22, -1, 1, 17 }
static double apsics_data [16]
static const cheb_series apsi_cs = { apsics_data, 15, -1, 1, 9 }

Detailed Description

Miscellaneous math functions

Definition in file MathFunctions.H.

Define Documentation

#define D_2_PI   6.2831853071795862319959269370883703

2*Pi

Definition at line 85 of file MathFunctions.H.

Referenced by gauss().

#define D_APERY   1.2020569031595942853997381615114499

Apery's Constant.

Definition at line 101 of file MathFunctions.H.

#define D_CATALAN   0.9159655941772190150546035149323841

Catalan's Constant.

Definition at line 93 of file MathFunctions.H.

#define D_DEGREE   0.0174532925199432957692369076848861

Number of radians in one degree.

Definition at line 89 of file MathFunctions.H.

#define D_E   2.7182818284590452353602874713526625

e

Definition at line 67 of file MathFunctions.H.

#define D_EULER_GAMMA   0.5772156649015328606065120900824024

The Euler-Mascheroni Constant (Not the same as e).

Definition at line 87 of file MathFunctions.H.

#define D_FRANSEN   2.8077702420285193652215011865577729

Fransén-Robinson constant.

Definition at line 105 of file MathFunctions.H.

#define D_GAUSS_KUZMAN   0.3036630028987326585974481219015562

Gauss-Kuzmin-Wirsing constant.

Definition at line 103 of file MathFunctions.H.

#define D_GLAISHER   1.2824271291006226368753425688697917

Glaisher-Kinkelin Constant.

Definition at line 95 of file MathFunctions.H.

#define D_GOLDEN_RATIO   1.6180339887498948482045868343656381

The golden ratio.

Definition at line 91 of file MathFunctions.H.

#define D_GOLOMB_DICKMAN   0.6243299885435508709929363831008372

Golomb-Dickman constant.

Definition at line 113 of file MathFunctions.H.

#define D_KHINCHIN   2.6854520010653064453097148354817956

Khinchin's Constant.

Definition at line 97 of file MathFunctions.H.

#define D_LOG_2   0.6931471805599453094172321214581766

Natural Log of 2 DEFINED in cmath as M_LN2, but is not 128 bit.

Definition at line 81 of file MathFunctions.H.

Referenced by wow().

#define D_LOG_2_PI   1.8378770664093454835606594728112353

Natural Log of 2*Pi.

Definition at line 77 of file MathFunctions.H.

#define D_LOG_PI   1.1447298858494001741434273513530587

Natural Log of Pi.

Definition at line 79 of file MathFunctions.H.

#define D_LOG_SQRT_2   0.3465735902799726547086160607290883

Natural Log of sqrt of 2.

Definition at line 83 of file MathFunctions.H.

Referenced by SurpriseModelSPC::surprise().

#define D_LOG_SQRT_2_PI   0.9189385332046727417803297364056176

Log Root of 2 Pi.

Definition at line 69 of file MathFunctions.H.

Referenced by lngamma().

#define D_MILL   1.3063778838630806904686144926026057

Mills' constant.

Definition at line 109 of file MathFunctions.H.

#define D_OMEGA   0.5671432904097838729999686622103555

Omega constant.

Definition at line 111 of file MathFunctions.H.

#define D_PI   3.1415926535897932384626433832795029

Miscellaneous math functions.

Constants 128 bits IEEE quad

Each constant is 128 bits IEEE quad. On a 64 bit system, a double is 128 bits. Thus, each number is a double on a modern system

# define M_El 2.7182818284590452353602874713526625L

is given for the value of 'e'. We follow this standard.

Note:

Definition at line 65 of file MathFunctions.H.

#define D_SERPINSKY   2.5849817595792532170658935873831711

Sierpin'ski's constant.

Definition at line 107 of file MathFunctions.H.

#define D_SOLDNER   1.4513692348833810502839684858920274

Ramanujan-Soldner's Constant.

Definition at line 99 of file MathFunctions.H.

#define D_SQRT_2   1.4142135623730950488016887242096981

Root of 2 DEFINED in cmath as M_SQRT2, but is not 128 bit.

Definition at line 75 of file MathFunctions.H.

Referenced by SurpriseModelSPC::surprise().

#define D_SQRT_2_PI   2.5066282746310002416123552393401041

Root of 2*Pi.

Definition at line 71 of file MathFunctions.H.

#define D_SQRT_PI   1.7724538509055160272981674833411451

Root of Pi.

Definition at line 73 of file MathFunctions.H.

#define L_2_PI   6.28318530717958647692528676655900576839433879875021164194988918461560L

2*Pi

Definition at line 140 of file MathFunctions.H.

#define L_CATALAN   0.91596559417721901505460351493238411077414937428167213426649811962176L

Catalan's Constant.

Definition at line 148 of file MathFunctions.H.

#define L_DEGREE   0.01745329251994329576923690768488612713442871888541725456097191440171L

Number of radians in one degree.

Definition at line 142 of file MathFunctions.H.

#define L_E   2.71828182845904523536028747135266249775724709369995957496696762772407L

e

Definition at line 124 of file MathFunctions.H.

#define L_EULER_GAMMA   0.57721566490153286060651209008240243104215933593992359880576723488486L

The Euler-Mascheroni Constant (Not the same as e).

Definition at line 144 of file MathFunctions.H.

#define L_GLAISHER   1.28242712910062263687534256886979172776768892732500119206374002174040L

Glaisher-Kinkelin Constant.

Definition at line 150 of file MathFunctions.H.

#define L_GOLDEN_RATIO   1.61803398874989484820458683436563811772030917980576286213544862270526L

The golden ratio.

Definition at line 146 of file MathFunctions.H.

#define L_KHINCHIN   2.68545200106530644530971483548179569382038229399446295305115234555721L

Khinchin's Constant.

Definition at line 152 of file MathFunctions.H.

#define L_LOG_2   0.69314718055994528622676398299518041312694549560546875000000000000000L

Natural Log of 2 DEFINED in cmath as M_LN2, but is not > 128 bit.

Definition at line 138 of file MathFunctions.H.

#define L_LOG_2_PI   1.83787706640934548356065947281123527972279494727556682563430308096553L

Natural Log of 2*Pi.

Definition at line 134 of file MathFunctions.H.

#define L_LOG_PI   1.14472988584940017414342735135305871164729481291531157151362307147214L

Natural Log of Pi.

Definition at line 136 of file MathFunctions.H.

#define L_LOG_SQRT_2_PI   0.91893853320467274178032973640561763986139747363778341281715154048276L

Log Root of 2 Pi.

Definition at line 126 of file MathFunctions.H.

#define L_PI   3.14159265358979323846264338327950288419716939937510582097494459230781L

Pi.

Constants 256 Bit

Each constant is 256 bits, This makes it a double long floating point on any modern 64 bit CPU.

Definition at line 122 of file MathFunctions.H.

#define L_SQRT_2   1.41421356237309514547462185873882845044136047363281250000000000000000L

Root of 2 DEFINED in cmath as M_SQRT2, but is not > 128 bit.

Definition at line 132 of file MathFunctions.H.

#define L_SQRT_2_PI   2.50662827463100050241576528481104525300698674060993831662992357634229L

Root of 2*Pi.

Definition at line 128 of file MathFunctions.H.

#define L_SQRT_PI   1.77245385090551602729816748334114518279754945612238712821380778985291L

Root of Pi.

Definition at line 130 of file MathFunctions.H.

Function Documentation

template<class T >
T acosec ( T  A  )  [inline]

inverse cosecant

Definition at line 316 of file MathFunctions.H.

References ASSERT.

template<class T >
T acosech ( T  A  )  [inline]

Inverse Hyperbolic Cosecant.

Definition at line 359 of file MathFunctions.H.

template<class T >
T acotan ( T  A  )  [inline]

inverse cotangent

Definition at line 324 of file MathFunctions.H.

template<class T >
T acotanh ( T  A  )  [inline]

Inverse Hyperbolic Cotangent.

Definition at line 366 of file MathFunctions.H.

template<class T >
T angDiff ( const T  A,
const T  B,
const double  diffWRAP = M_PI 
) [inline]

Angle difference, which is the minimum circular difference between two angles. Angles are in rad. Only for angles from 0 to diffWRAP.

Definition at line 421 of file MathFunctions.H.

References min().

template<class T >
double angle ( const Point2D< T >  p0,
const Point2D< T >  p1,
const Point2D< T >  p2 
) [inline]

Find the cosine of the angle between two vectors (p0,p1) and (p0,p2).

Definition at line 428 of file MathFunctions.H.

References Point2D< T >::i, and sqrt().

Referenced by BeoLRF::evolve(), BeoSubDB::getDirections(), MiddleTemporal::getMTfeaturesDisplay(), ContourChannel::getSubmapName(), ContourChannel::getSubmapNameShort(), VectorHistField::obstacleTemplate(), and BeoSubBin::pruneLines().

template<class T >
T asec ( T  A  )  [inline]

inverse secant

Definition at line 308 of file MathFunctions.H.

References ASSERT.

template<class T >
T asech ( T  A  )  [inline]

Inverse Hyperbolic Secant.

Definition at line 352 of file MathFunctions.H.

template<class T , class T2 >
T clampValue ( const T &  val,
const T2 &  bound1,
const T2 &  bound2 
) [inline]

Returns the number closest to val and between bound1 and bound2.

The bounds may be specified in either order (i.e., either (lo, hi) or (hi, lo).

Definition at line 561 of file MathFunctions.H.

Referenced by DirectFeedChannel::clampCoeffs(), drawMeters(), fromVideoYUV422P(), and warp3D().

template<class T >
T cosec ( T  A  )  [inline]

Cosecant.

Definition at line 294 of file MathFunctions.H.

template<class T >
T cosech ( T  A  )  [inline]

Hyperbolic Cosecant.

Definition at line 338 of file MathFunctions.H.

template<class T >
T cotan ( T  A  )  [inline]

Cotangent.

Definition at line 301 of file MathFunctions.H.

template<class T >
T cotanh ( T  A  )  [inline]

Hyperbolic Cotangent.

Definition at line 345 of file MathFunctions.H.

double expdev ( int &  idum  ) 

Randomly distributed Exponential deviate.

Definition at line 204 of file MathFunctions.C.

References log(), and ran2().

template<class T >
T gamma ( T  X,
const T  A,
const T  B 
) [inline]

find p from a gamma distrabution

Definition at line 473 of file MathFunctions.H.

References exp().

Referenced by ImageSpring< T >::computePos(), and HMM< T >::train().

double gasdev ( int &  idum  ) 

Randomly distributed Gaussian deviate with zero mean and unit variance.

Definition at line 181 of file MathFunctions.C.

References log(), ran2(), and sqrt().

template<class T >
T gauss ( T  diff,
const T  Std 
) [inline]

find p from a Gaussian distribution (instead of the mu and A, the difference is supplied)

Definition at line 463 of file MathFunctions.H.

References D_2_PI, exp(), and fastSqrt().

template<class T >
T gauss ( T  A,
const T  Mu,
const T  Std 
) [inline]

find p from a Gaussian distribution

Definition at line 452 of file MathFunctions.H.

References D_2_PI, exp(), and fastSqrt().

Referenced by L2GMM().

double getChi2Inv ( int  k  )  [inline]

A table for returning the chi2inv at 95% (should be expanded as needed).

Definition at line 1181 of file MathFunctions.H.

Point2D<float> getEllipseFromCov ( const Image< double > &  cov  ) 

Convert from a covariance matrix to the major/minor axis of an ellipse.

Definition at line 295 of file MathFunctions.C.

References ASSERT, Image< T >::getHeight(), Image< T >::getVal(), Image< T >::getWidth(), sqrt(), and trace().

int getIdum ( const bool  useRandom = true  ) 

Get a random seed for ran2.

If useRandom is true, a random negative number will be return, otherwise a negative number that is always the same will be returned.

Definition at line 172 of file MathFunctions.C.

void initRandomNumbers (  ) 

Initialize random seeds from pseudo-random sources (e.g. time(), getpid()).

Definition at line 68 of file MathFunctions.C.

Referenced by BeeStemSim::BeeStemSim(), main(), ModelManager::paramChanged(), SceneGenerator::SceneGenerator(), Staircase::start2(), ObjRec::start2(), and submain().

void initRandomNumbersZero (  ) 

Initialize random seeds with zero, to produce deterministic pseudo-random sequences.

Definition at line 77 of file MathFunctions.C.

Referenced by ModelManager::paramChanged().

template<class T >
bool isBounded ( T  A,
const T  upper,
const T  lower 
) [inline]

find if this value or pixel is bounded by the other two

Definition at line 498 of file MathFunctions.H.

bool isFinite ( const double &  arg  ) 

Function to check for finite value.

Definition at line 51 of file MathFunctions.C.

bool isFinite ( const float &  arg  ) 

Function to check for finite value.

Definition at line 50 of file MathFunctions.C.

bool isFinite ( const int32 &  arg  ) 

Function to check for finite value.

Definition at line 47 of file MathFunctions.C.

bool isFinite ( const int16 &  arg  ) 

Function to check for finite value.

Definition at line 46 of file MathFunctions.C.

bool isFinite ( const byte &  arg  ) 

Function to check for finite value.

Definition at line 45 of file MathFunctions.C.

template<class T >
T KLgamma ( const T  a,
const T  A,
const bool  doWow = false 
) [inline]

Compute the KL distance for a single gamma PDF.

Here we fix beta to be 1. This is a special case, but if we have it we can compute KL much faster. We can also use this if beta1 = beta2 The Chi Square is one such case where beta is 1/2 .

Parameters:
a New Alpha
A Current Alpha
doWow is true then convert output to Wows

Definition at line 1047 of file MathFunctions.H.

References wow().

template<class T >
T KLgamma ( const T  a,
const T  b,
const T  A,
const T  B,
const bool  doWow = false 
) [inline]

Compute the KL distance for a single gamma PDF.

Parameters:
a New Alpha
b New Beta
A Current Alpha
B Current Beta
doWow is true then convert output to Wows

Definition at line 939 of file MathFunctions.H.

References fastLog(), and wow().

Referenced by KLjointGammaGamma(), and KLjointGammaGauss().

template<class T >
T KLgammaConst ( const T  a,
const T  A,
const T  C1,
const T  C2,
const bool  doWow = false 
) [inline]

Compute the KL distance for a single gamma PDF.

This method produces the best results for usage with RSVP data as measured by the MAG when using the example values for C1 and C2. It is also faster than the basic KL computation since we eliminate two divisions and one log computation.

Parameters:
a New Alpha
A Current Alpha
C1 the const standin for B/b - 1
C2 the const standin for log(b/B)
doWow is true then convert output to Wows

Definition at line 988 of file MathFunctions.H.

References wow().

template<class T >
T KLgauss ( const T  u,
const T  s,
const T  U,
const T  S,
const bool  doWow = false 
) [inline]

Compute the KL distance for a single gauss PDF.

Parameters:
u New Mean
s New Std.
U Current Mean
S Current Std.
doWow is true then convert output to Wows

Definition at line 1070 of file MathFunctions.H.

References log(), and wow().

Referenced by KLjointGammaGauss().

template<class T >
T KLjointGammaGamma ( const T  ai,
const T  aj,
const T  bi,
const T  bj,
const T  Ai,
const T  Aj,
const T  Bi,
const T  Bj,
const bool  doWow = false,
const T  gammaBiasi = 1.0F,
const T  gammaBiasj = 1.0F 
) [inline]

Compute the KL distance for a joint gamma PDF.

Parameters:
ai New Alpha in model i
aj New Alpha in model j
bi New Beta in model i
bj New Beta in model j
Ai Current Alpha in model i
Aj Current Alpha in model j
Bi Current Beta in model i
Bj Current Beta in model j
doWow is true then convert output to Wows

This formula derived by T. Nathan Mundhenk 2007

Definition at line 823 of file MathFunctions.H.

References KLgamma(), and wow().

template<class T >
T KLjointGammaGauss ( const T  a,
const T  u,
const T  b,
const T  s,
const T  A,
const T  U,
const T  B,
const T  S,
const bool  doWow = false,
const T  gammaBias = 1.0F,
const T  gaussBias = 1.0F 
) [inline]

Compute the KL distance for a joint gamma gauss PDF.

Parameters:
a New Alpha in model 1
b New Beta in model 1
u New Mean in model 2
s New Std. in model 2
A Current Alpha in model 1
B Current Beta in model 1
U Current Mean in model 2
S Current Std. in model 2
doWow is true then convert output to Wows

This formula derived by T. Nathan Mundhenk 2007

Definition at line 887 of file MathFunctions.H.

References KLgamma(), KLgauss(), and wow().

double L2GMM ( const std::vector< GaussianDef > &  f,
const std::vector< GaussianDef > &  g 
) [inline]

Compute the L2 distance between two mixtures of Gaussians.

Parameters:
f GMM1
g GMM2

Definition at line 1124 of file MathFunctions.H.

References gauss().

double lngamma ( double  x  ) 

Compute log of Gamma.

Definition at line 215 of file MathFunctions.C.

References D_LOG_SQRT_2_PI, and log().

Referenced by poisson().

template<class T >
T logN ( T  A,
const T  n 
) [inline]

logN for pixel

Definition at line 382 of file MathFunctions.H.

References log().

template<class T >
T logsig ( T  A,
const T  a,
const T  b 
) [inline]

log sigmoid for pixel

Definition at line 392 of file MathFunctions.H.

References exp().

Referenced by featureClusterVision< FLOAT >::fCVrunStandAloneMSBatchTest().

template<class T >
T logsig2 ( T  x,
const T  a,
const T  b 
) [inline]

log sigmoid for pixel with offset

Values like a = 10 and b = 5 create a nice sigmoid for x = 0 to 1 since the center of the sigmoid is at b/a.

Parameters:
a The slope for the sigmoid
b The offset for the sigmoid

Definition at line 405 of file MathFunctions.H.

References exp().

Referenced by H2SVChannel::doInput().

template<class T >
T max ( T  A  )  [inline]

this nonsense operator is for compatability

Definition at line 484 of file MathFunctions.H.

Referenced by approximateHull(), lobot::LRFData::average_distance(), BlurFoveator::BlurFoveator(), centerSurround(), centerSurroundDiff(), centerSurroundDiffSingleOpponent(), centerSurroundSingleOpponent(), RecurBayes::classify(), Bayes::classify(), Bayes::classifyRange(), SimulationViewerStats::computeAGStats(), convertFromString(), cudaCenterSurround(), cudaCenterSurroundDiff(), cudaCenterSurroundSingleOpponent(), cudaIsDyadic(), dilateImg(), BitObject::doesIntersect(), TemplateMatchChannel::drawResults(), erodeImg(), Gist_Navigation::evolve(), BeoLRF::evolve(), findPeaks(), LPTFoveator::foveate(), BlurFoveator::foveate(), SimTime::fromString(), FrameRange::fromString(), lobot::OccGrid::get(), getAugmentedBeliefBayesImage(), ImageSpring< T >::getClusteredImage(), GistEstimatorGen::getGistImage(), RawGistEstimatorStd::getGistImage(), VisualObjectMatch::getMatchImage(), Graph::getMaxDirectedDistance(), VisualEvent::getMaxObjectDims(), Graph::getMaxUndirectedDistance(), Beowulf::getNbSlaves(), TopologicalMap::getNodeSegmentMaxDistance(), VisualObjectDB::getObjectMatches(), Rectangle::getOverlap(), Image< T >::getValInterpScaled(), goodness_map(), VCC4::gotoPosition(), HmaxFL::init(), CudaHmaxFL::init(), SurpriseMap< T >::initModels(), LPTFoveator::invLPT(), junctionFilterFull(), ParamMap::load(), main(), SimTime::MAX(), rutz::mutex_atomic_int::max_value(), rutz::darwin_atomic_int::max_value(), maxNormalizeFancy(), maxNormalizeFancyFast(), maxNormalizeFancyLandmark(), maxNormalizeLandmark(), MSTFilterFull(), LogLikelihoodClassifier::nearestNeighborVotePDF(), DisparityChannel::normalizeDispMap(), normalizeFloat(), normalizeFloatRgb(), normalizeRGPolar(), normalizeRGPolarAuto(), normalizeScaleRainbow(), normalizeWithScale(), Range< T >::operator==(), LogLikelihoodClassifier::predict(), LogLikelihoodClassifier::predictPDF(), lobot::Compositor< pixel_type >::push_back(), BPnnet::recognize(), CudaSaliency::runSaliency(), SimulationViewerStats::saveAGMaskStats(), SimulationViewerStats::saveCompat(), SimulationViewerNerdCam::saveResults(), SingleChannel::saveStats(), LPTFoveator::setOrigin(), ScaleRemoveSurprise< FLOAT >::SRSsetAntiWeightsInteract(), SurpriseMapFFT< T >::surprise(), VisualTracker::trackObjects(), lobot::FastSLAM::update(), WeightFinder::visitComplexChannel(), JetFiller::visitSingleChannel(), WeightFinder::visitSingleChannel(), SDLdisplay::waitNextRequestedFrameTime(), and warp3D().

template<class T >
T mean ( T  A  )  [inline]

this nonsense operator is for compatability

Definition at line 512 of file MathFunctions.H.

template<class T >
T min ( T  A  )  [inline]

this nonsense operator is for compatability

Definition at line 491 of file MathFunctions.H.

Referenced by angDiff(), approximateHull(), lobot::LRFData::average_distance(), centerSurround(), centerSurroundDiff(), centerSurroundDiffSingleOpponent(), centerSurroundSingleOpponent(), chamfer34(), SimulationViewerStats::computeAGStats(), constrainRect(), DPM::convolveModel(), ColorHist::createFeatureVector(), LocalBinaryPatterns::createRawHistogram(), cudaCenterSurround(), cudaCenterSurroundDiff(), cudaCenterSurroundSingleOpponent(), cudaCrop(), damerauLevenshteinDistance(), dispResults(), BitObject::doesIntersect(), VarianceChannel::doInput(), PN03contrastChannel::doInput(), EntropyChannel::doInput(), TemplateMatchChannel::drawResults(), BeoLRF::evolve(), featurePoolHmax(), SimTime::fromString(), lobot::OccGrid::get(), getAugmentedBeliefBayesImage(), HmaxFL::getC2(), CudaHmaxFL::getC2(), TopologicalMap::getDistance(), Geons3D::getEdgeProb(), TopologicalMap::getMapImage(), Graph::getMaxDirectedDistance(), Graph::getMaxUndirectedDistance(), TopologicalMap::getNodeSegmentMaxDistance(), TcorrChannel::getOutput(), SpectralResidualChannel::getOutput(), Rectangle::getOverlap(), TopologicalMap::getPath(), Image< T >::getValInterp(), VCC4::gotoPosition(), inplaceAddBGnoise2(), levenshteinDistance(), logmagnitude(), main(), maxNormalizeFancy(), maxNormalizeFancyLandmark(), multilinePlot(), DisparityChannel::normalizeDispMap(), normalizeRGPolarAuto(), normalizeScaleRainbow(), normalizeWithScale(), NPclassify2< FLOAT >::NPgetStemNumberEdit(), Range< T >::operator==(), SpatialMetrics::paramChanged(), CudaSaliency::runSaliency(), SimulationViewerStats::saveAGMaskStats(), SimulationViewerStats::saveCompat(), SimulationViewerNerdCam::saveResults(), SingleChannel::saveStats(), spatialPoolMax(), ScaleRemoveSurprise< FLOAT >::SRSsetAntiWeightsInteract(), takeMin(), VisualTracker::trackObjects(), JetFiller::visitSingleChannel(), and warp3D().

template<class T >
T onlineMean ( T  mu,
T  A,
int  n 
) [inline]

Compute the mean online by supplying the current mean and a new value mu is the previous mean, A is the current value and n is the number of values proceses so far

Definition at line 527 of file MathFunctions.H.

Referenced by HeliPose::getIMUBias().

double poisson ( const unsigned int  k,
const double  mu 
)

Compute probability of drawing a value k from a Poisson of mean mu.

Definition at line 250 of file MathFunctions.C.

References exp(), lngamma(), and log().

Referenced by SurpriseModelOD::surprise().

double psi ( const double  x  )  [inline]

Compute the psi (derivarive of log of gamma) function (requires x > 0.0).

Definition at line 735 of file MathFunctions.H.

References fastLog().

Referenced by gaborFilter(), gaborFilter2(), gaborFilter3(), and grating().

double ran2 ( int &  idum  ) 

Random number generator from Numerical Recipes in C book.

Long period >2x10^18 random number generator of L Ecuyer with Bays-Durham shuffle. Return a uniform deviate in the interval (0,1). Call with int variable as argument set to a negative value, and don't change this variable between calls unless you want to reseed the generator. You can get ain initial seed using the function getIdum()

Definition at line 130 of file MathFunctions.C.

Referenced by expdev(), and gasdev().

double randomDouble (  ) 

Generate a random double in [0.0,1.0).

This is a thin wrapper around drand48() or rand(), depending on which is available on the build platform.

Definition at line 86 of file MathFunctions.C.

Referenced by WTAwinner::buildFromSMcoords(), Staircase::getValues(), inplaceAddBGnoise2(), inplaceSpeckleNoise(), main(), randomDoubleFromNormal(), BPnnet::randomizeWeights(), randomUpToNotIncluding(), HippocampusI::resampleParticles(), and Beowulf::send().

double randomDoubleFromNormal ( const double  s  ) 

Generate a random double from a normal distribution with mean zero and standard deviation s.

This function call randomDouble() 12 times to sample from normal distribution

Definition at line 96 of file MathFunctions.C.

References randomDouble(), and sum().

Referenced by Objects::proposeState(), and HippocampusI::updateParticleMotion().

int randomUpToIncluding ( const int  n  ) 

Generate a random integer in [0,n] (i.e., including n).

This is a thin wrapper around lrand48() or rand(), depending on which is available on the build platform.

Definition at line 106 of file MathFunctions.C.

References randomUpToNotIncluding().

Referenced by ArmPlanner::gibbsSampling(), inplaceColorSpeckleNoise(), main(), randArmMove(), and SimulationViewerEyeRegion::start1().

int randomUpToNotIncluding ( const int  n  ) 

Generate a random integer in [0,n) (i.e., not including n).

This is a thin wrapper around lrand48() or rand(), depending on which is available on the build platform.

Definition at line 112 of file MathFunctions.C.

References randomDouble().

Referenced by PsychoDisplay::displayEyeTrackerCalibration(), ImageSpring< T >::getStats(), ImageSpring< T >::getStatsDist(), SimulationViewerCompress::getTraj(), inplaceColorSpeckleNoise(), main(), randomUpToIncluding(), randShuffle(), SimulationViewerStats::save1(), and submain().

template<class T >
void randShuffle ( T *  array,
const uint  size 
) [inline]

Randomly shuffle given array.

Definition at line 577 of file MathFunctions.H.

References randomUpToNotIncluding().

Referenced by PsychoDisplay::displayNumbers(), main(), and submain().

template<class T >
T saturate ( T  A,
const T  n 
) [inline]

saturate pixel at some value

Definition at line 443 of file MathFunctions.H.

template<class T >
T sec ( T  A  )  [inline]

Secant.

Definition at line 287 of file MathFunctions.H.

Referenced by BufferedFrameIstream::startStream(), Staircase::stop1(), EventLog::stop2(), EyeTrackerISCAN::stopTracking(), and submain().

template<class T >
T sech ( T  A  )  [inline]

Hyperbolic Secant.

Definition at line 331 of file MathFunctions.H.

template<class T >
T sign ( T  A  )  [inline]

return the sign of this item

Definition at line 373 of file MathFunctions.H.

template<class T >
int signOf ( const T &  x  )  [inline]

Returns -1 if x is negative, or 1 if x is positve.

Definition at line 554 of file MathFunctions.H.

template<class T >
T squareOf ( const T &  x  )  [inline]

Returns the square of x.

Definition at line 557 of file MathFunctions.H.

Referenced by avgOrient(), GeometricHashing::changeBasis(), corrcoef(), drawDiskCheckTarget(), DPM::dtHelper(), ImageSpring< T >::getClusteredImage(), ImageSpring< T >::getDistanceMasses(), Scorbot::getIKArmPos(), SoxChannel::getNonlinearResponse(), ImageSpring< T >::getStatsDist(), Scorbot::gravityComp(), and HippocampusI::updateParticleSlamObservation().

template<class T >
T sum ( T  A  )  [inline]

this nonsense operator is for compatability

Definition at line 505 of file MathFunctions.H.

template<class T >
T tansig ( T  A  )  [inline]

tan sigmoid for pixel

Definition at line 413 of file MathFunctions.H.

References exp().

template<class T >
T wow ( const T &  k  )  [inline]

Convert a number into Wows, for instance a KL distance.

Wow's in this computation is the same as the conversion from Nats to Bits in KL

Definition at line 796 of file MathFunctions.H.

References D_LOG_2.

Referenced by KLgamma(), KLgammaConst(), KLgauss(), KLjointGammaGamma(), and KLjointGammaGauss().

Variable Documentation

double apsics_data[16] [static]
Initial value:
 {
  -.0204749044678185,
  -.0101801271534859,
   .0000559718725387,
  -.0000012917176570,
   .0000000572858606,
  -.0000000038213539,
   .0000000003397434,
  -.0000000000374838,
   .0000000000048990,
  -.0000000000007344,
   .0000000000001233,
  -.0000000000000228,
   .0000000000000045,
  -.0000000000000009,
   .0000000000000002,
  -.0000000000000000
}

Definition at line 650 of file MathFunctions.H.

double psics_data[23] [static]
Initial value:
 {
  -.038057080835217922,
   .491415393029387130,
  -.056815747821244730,
   .008357821225914313,
  -.001333232857994342,
   .000220313287069308,
  -.000037040238178456,
   .000006283793654854,
  -.000001071263908506,
   .000000183128394654,
  -.000000031353509361,
   .000000005372808776,
  -.000000000921168141,
   .000000000157981265,
  -.000000000027098646,
   .000000000004648722,
  -.000000000000797527,
   .000000000000136827,
  -.000000000000023475,
   .000000000000004027,
  -.000000000000000691,
   .000000000000000118,
  -.000000000000000020
}

Definition at line 622 of file MathFunctions.H.

Generated on Sun May 8 08:42:52 2011 for iLab Neuromorphic Vision Toolkit by  doxygen 1.6.3